本文目录一览:
嫦娥6号轨道是韦神计算的吗
1、嫦娥6号的轨道不是韦神计算的。虽然韦神在数学领域有卓越的成就,但航天任务的计算是一个涉及多学科合作的复杂系统工程,包括但不限于数学、物理和工程学等。嫦娥6号的轨道计算需要考虑到多重变轨、地球和月球之间的引力关系、发射时的环境因素以及航天器自身的性能等多种因素。
航天器轨道六要素和TLE两行轨道数据格式
1、TLE两行轨道数据格式TLE(Two-Line Orbital Element)两行轨道数据,是用于描述航天器轨道信息的简洁格式。它由两行数据组成,每行包含多个字段,分别表示航天器的不同轨道参数。以下是TLE两行轨道数据格式的详细介绍:Line 0(非标准行,但通常包含)Columns 1-24:卫星通用名称,基于卫星目录的信息。
2、航天器轨道的六要素包括:半长轴a、偏心率e、轨道倾角i、升交点赤经、近地点辐角、过近地点时刻或真近点角。这些要素共同决定了航天器的运动轨迹。半长轴a:轨道长轴的一半,与偏心率e一起决定了轨道的形状。偏心率e:描述椭圆形状的离心程度,同样影响轨道的形状。
3、航天器的运动轨迹由六要素决定,这些要素在TLE的两行数据中表示。
4、星历,或称两行轨道数据(TLE),是卫星、航天器或飞行体进入太空后,由美国的CelesTrak发明的一种描述其轨道位置和速度的数据形式。卫星一旦进入NORAD卫星星历编号目录,将被终生跟踪,即便成为太空垃圾,直至目标消失。
5、星历,也叫两行轨道数据(TLE,Two-Line Orbital Element),是由美国的CelesTrak发明的,用于描述卫星、航天器或飞行体在太空中的位置和速度信息。卫星、航天器或飞行体一旦进入太空,即被列入NORAD(North American Aerospace Defense Command,北美防空司令部)卫星星历编号目录,并被终生跟踪。
6、卫星星历的一种常见形式是两行轨道数据,由美国celestrak发明创立。TLE以两行简洁的数据形式,提供了描述太空飞行体位置和速度所需的全部信息。综上所述,卫星星历是航天活动中不可或缺的重要工具,它为我们提供了精确、可靠的卫星等飞行体的运行状态信息,为航天活动的安全、有效进行提供了有力保障。
轨道六根数
卫星的轨道六根数是STK基础知识中至关重要的概念,它决定了卫星在空间中的确切位置。在STK软件中进行卫星轨道信息设置时,这六个参数是必不可少的。第一个参数负责表示轴向信息,用于定义轨道的长度,即卫星轨道的大小,通常在工程实践中使用半长轴。
综上所述,轨道六根数是描述天体或航天器在开普勒轨道上运动时必要的六个参数,它们共同确定了轨道的大小、形状、位置和方向。
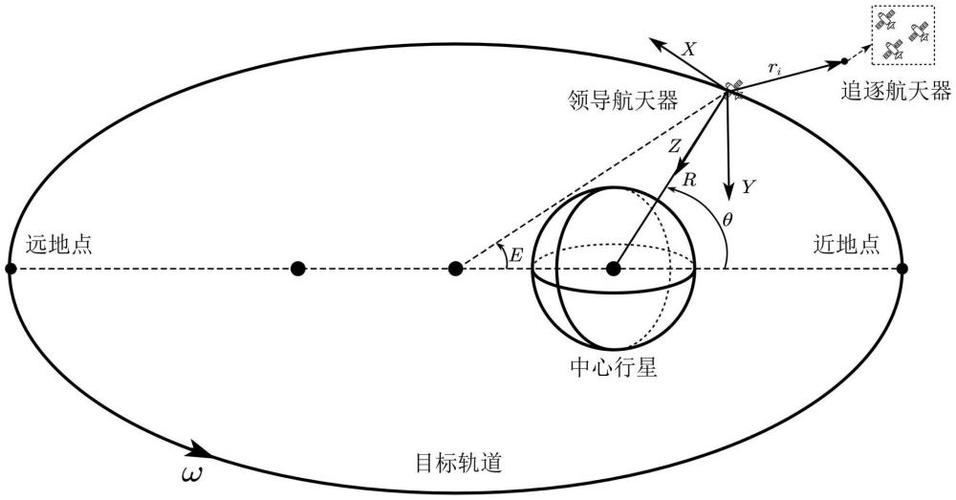
轨道六根数是用于描述航天器沿着轨道在某一时刻的位置的一组参数。它们分别是半长轴a、偏心率e、轨道倾角i、升交点赤经RAAN、近地点幅角ω与真近点角f。以下是每个参数的具体意义:半长轴(Semimajor Axis,a)定义:椭圆轨道长轴的一半,用于描述椭圆的大小。
卫星轨道六根数保姆级科普学习笔记卫星轨道六根数是描述卫星在空间中运动状态的重要参数,它们分别是:轨道半长轴(a)、轨道偏心率(e)、轨道倾角(i)、近地点幅角(ω)、升交点赤经(Ω)和平近点角(M)。下面将对其中较为复杂的近地点幅角和升交点赤经进行详细解释,并通过图片辅助理解。
STK中的轨道六根数决定了卫星在空间中的确切位置,以下是其详细介绍:半长轴:定义:表示轨道的长度,即卫星轨道的大小。作用:在工程实践中,半长轴用于定义卫星轨道的主要尺寸。短半轴:定义:专门用于定义较短轴的长度。作用:与半长轴共同决定轨道的形状,即轨道的扁平程度。
轨道六根数,即轨道要素或轨道参数,是描述天体或航天器在开普勒轨道上运动所必需的六个基本参数。以下是轨道六根数的简要介绍:半长轴:描述轨道椭圆形状的大小,即椭圆两个焦点到椭圆上任意一点的距离之和的一半。偏心率:描述轨道椭圆的形状,其值在0到1之间。
卫星变轨所需变速量如何计算
1、其实你需要计算的是200×500公里轨道的近地点速度,然后减去200公里圆轨道上的速度。注意一下,R表示轨道半径,需要在轨道高度之上加上地球半径。具体不帮你计算了,高中水平就可以。答案是:838米/秒。用这个方法还可以用近地点速度和高度计算远地点速度和高度。
2、卫星首先加速,沿着椭圆轨道移动到远地点,然后减速,进入半径为R的圆形轨道。变轨过程只经过椭圆轨道的一半。假设卫星在半径为r的初始轨道上的运行周期为T0,卫星质量为m,可得公式:GMm/r2=m4π2/(r*T02)。由此可推导出:T0=(4π2 *r3)/GM)1/2。
3、所需向心力$F = frac{mv^2}{r}$减小,万有引力大于卫星所需的向心力。卫星将做向心运动,轨道半径变小。进入新轨道后,由$v = sqrt{frac{GM}{r}}$可知,运行速度增大,但重力势能、机械能均减少。
轨道确定简介
轨道确定是航天器运行管理中的关键环节,它涉及从测量数据中精确确定航天器的飞行路径。以下是轨道确定的简介: 数据获取与预处理 数据来源:轨道确定的过程始于数据的获取,这些数据主要来自于航天飞行控制中心的各种观测设备。 数据类型:收集的数据包括航天器的位置、速度、加速度等信息。
人造地球卫星轨道的确定:卫星在轨道上绕地球卫星主要是由发射时提供的能量,给了卫星相应的速度,这个速度的大小和方向决定了轨道的高度,另外卫星也可以携带燃料,在绕地球运行的过程中进行变轨制动,以改变速度的方式改变轨道高度。
轨道是指卫星在太空中固定的运动路线,就像火车沿着铁轨行驶一样。当火车离开轨道时,它会出轨,引发事故。同样地,卫星在太空中也会沿着预定的轨道运行。我们能够计算出未来几天或几年内卫星的具体位置。卫星本身并不具备持续的动力来源,在发射卫星的火箭将其送入太空时,会提供一个初始速度。
轨道确定基本理论主要包括轨道误差估算理论、航天器轨道运动理论以及计算方法。 轨道误差估算理论 是轨道改进的核心,旨在通过精确分析观测数据来确定航天器的真实位置。 常用方法包括批量估算法和序贯估算法。
第一宇宙速度的推导公式是什么?
其中,(G)为万有引力常数,(M_{地})为地球质量,(m)为物体质量,(r_{地})为地球半径,(v_{1})为第一宇宙速度。
第一宇宙速度公式V=√gR的推导过程如下:依据牛顿第二定律:物体的加速度与作用在其上的合力成正比,即F=ma。考虑地球对质点的引力:根据万有引力定律,地球对质点的引力为F=mg,其中m代表质点的质量,g为重力加速度。将引力表达式代入牛顿第二定律中,得到mg=ma,质量m可以约去,得到g=a。
第一宇宙速度推导公式就是F=GMm/r=mv/r又这个公式我们可以得出GM=gr。从而解得v=gr,将R地=37×10m,g=8 m/s代入,并开平方,得v= 9 km/s。其中F为两个物体之间的引力,G是万有引力常数,r则是两个物体之间的距离。mg=mv^2/r,解得v=√gr,约是每秒9千米。
本文来自作者[runkeda]投稿,不代表润科号立场,如若转载,请注明出处:https://www.runkeda.cn/shehui/202509-16769.html







评论列表(3条)
我是润科号的签约作者“runkeda”
本文概览:本文目录一览: 1、嫦娥6号轨道是韦神计算的吗 2、...
文章不错《航天器轨道计算(航天器轨道的划分标准包括)》内容很有帮助